Back to projectPublic page

Fourier Series Approximations

This section is still being documented. Clone the project to customize it or keep reading for context.

Part of Visual Mathematics Project

4 blocks0 nested pages

Browse project

Last updated Jan 30, 2026. Clone to remix or explore the blocks below.

2d89b9af...

79a1cb96...

examples

Frequencies Everywhere

From MP3s to Instagram filters

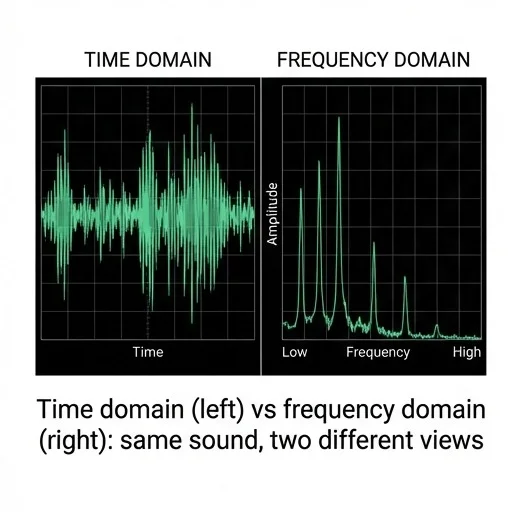
Side-by-side comparison of time domain waveform and frequency domain spectrum showing peaks at different frequencies

Click to zoom

Time domain (left) vs frequency domain (right): same sound, two different views

Audio equalizer with multiple frequency sliders showing bass, mid, and treble controls

Click to zoom

Equalizer: each slider controls one frequency range independently (Fourier components)

Original high-quality image next to JPEG compressed version showing slight quality loss

Click to zoom

JPEG compression: remove high frequencies humans barely notice, keep low frequencies

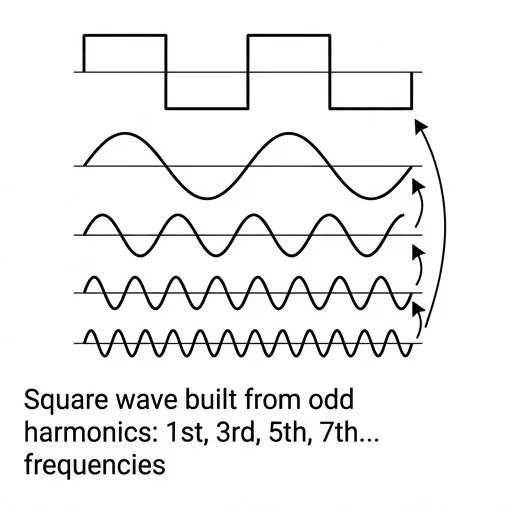
Visual showing multiple sine waves of different frequencies adding up to approximate a square wave

Click to zoom

Square wave built from odd harmonics: 1st, 3rd, 5th, 7th... frequencies

adc852fc...

concept

🎵 How Your Phone Stores 1000 Songs

Your voice saying "hello" contains maybe 50 different frequencies mixed together.

MP3 compression: break the sound into frequencies, delete the ones you can't hear (above 20kHz, below 20Hz), keep the rest.

Result: 10% of original size, sounds identical.

The math behind this? Fourier decomposition — the visualization above.

6dda3d78...

quiz

Apply Fourier Thinking

Think in frequencies for audio and images

0 / 8

In the visualization, adding more circles (more terms in the Fourier series) makes the approximation better. Mathematically, the infinite series $\sum_{n=1}^{\infty}$ converges to the exact square wave. In practice, why stop at finite terms?