Back to projectPublic page

3d Surface In Calculus

This section is still being documented. Clone the project to customize it or keep reading for context.

Part of Visual Mathematics Project

4 blocks0 nested pagescreate

Browse project

Last updated Jan 29, 2026. Clone to remix or explore the blocks below.

6ecad9a8...

37765791...

Image

Real-World Examples

Parabolas, saddles, and contours in everyday objects

Satellite dish showing parabolic curve with parallel incoming waves reflecting to focal point

Click to zoom

Satellite dish: parallel radio waves reflect to one focal point due to parabolic shape

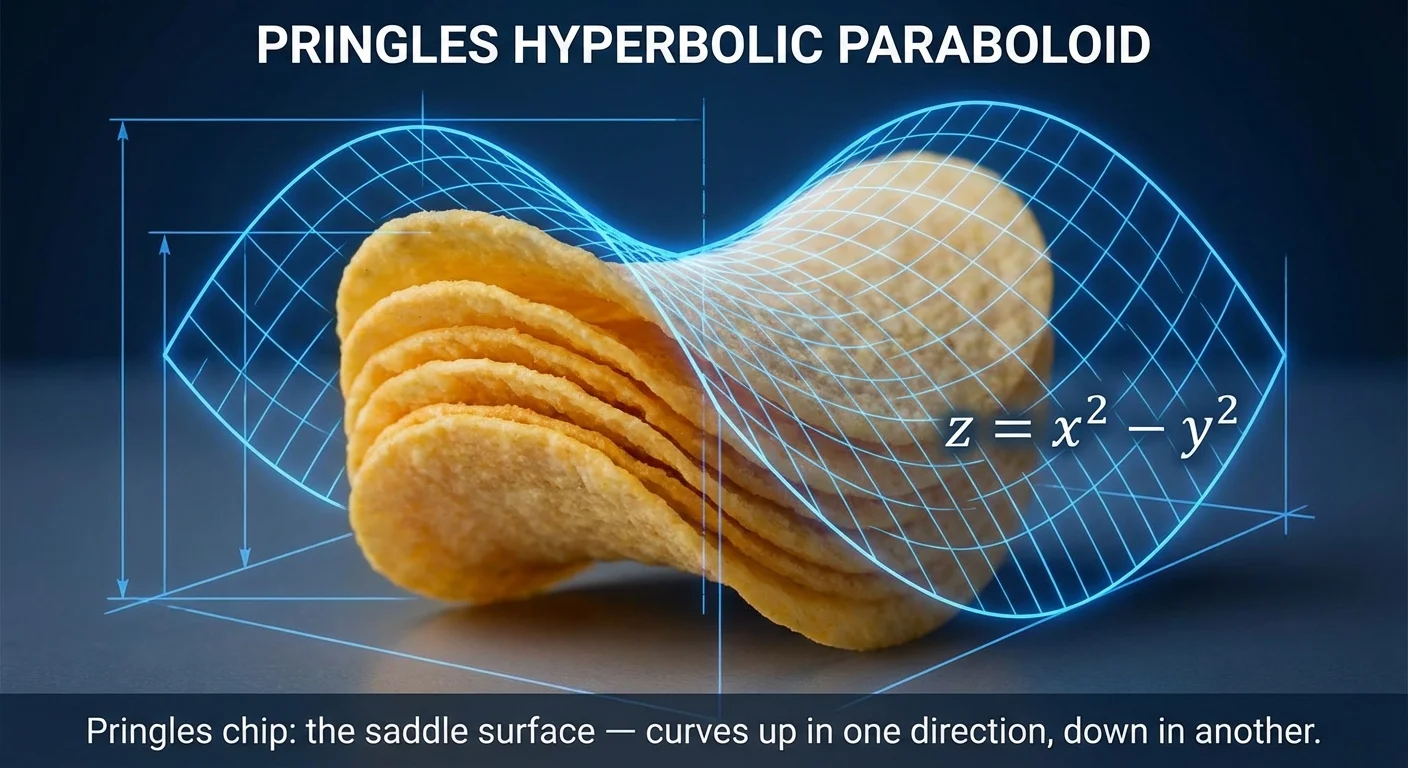
Pringles potato chip photographed to show hyperbolic paraboloid saddle curve

Click to zoom

Pringles chip: the saddle surface $z = x^2 - y^2$ — curves up in one direction, down in another

Topographic hiking map showing contour lines around a mountain peak with elevation labels

Click to zoom

Topographic map: each contour line connects points at the same elevation

Power plant cooling tower with distinctive saddle-shaped hyperbolic paraboloid structure

Click to zoom

Cooling tower: saddle shape distributes structural forces efficiently

fd61727b...

concept

3D Surfaces

Functions with two inputs and their geometry

🗺️ Google Maps Knows Your Elevation

You're at latitude 28.6139, longitude 77.2090 (Delhi). Google Maps shows: elevation 216 meters.

How? Every (latitude, longitude) pair maps to exactly one elevation value. That's a function with two inputs producing one output: $z = f(x, y)$

Now rotate the 3D surface above. Every point $(x, y)$ on the floor has a height $z$ . Collect all these heights and you get the surface.

This is multivariable calculus — understanding functions where multiple inputs affect the output.

edb81121...

quiz

Apply the Concepts

Test your understanding of multivariable functions

0 / 7

You're building a pricing model: revenue $= f($ price, ad_budget $)$ . You calculate $\frac{\partial \, \mathrm{revenue}}{\partial \, \mathrm{price}} = -50$ . What does this mean?