Back to projectPublic page

1. A Square And A Cube

This section is still being documented. Clone the project to customize it or keep reading for context.

Part of NCERT 8 Math

6 blocks1 nested pagecreate

Browse project

Last updated Jan 18, 2026. Clone to remix or explore the blocks below.

381f4775...

prerequisite

Prior Knowledge Check

Essential concepts you should know before starting

0 of 6 completedSyncing saved progress…0%

Before You Start: Do You Know These?

ddb1b88f...

bcdf419a...

visualize

Count in L-shapes, discover squares

Instead of counting row by row, count in L-shaped layers from the corner. Each layer adds an odd number of cells — and the running total is always a perfect square. Look at the top row of the grid. What's special about them!

Layer by layer

1 = 1 = 1²

1 + 3 = 4 = 2²

1 + 3 + 5 = 9 = 3²

1 + 3 + 5 + 7 = 16 = 4²

1 + 3 + 5 + 7 + 9 = 25 = 5²

▶ Start

First row = perfect squares

Empty grid

f40ca9fc...

story

The Queen's Locker Puzzle

An ancient puzzle about lockers, factors, and perfect squares

Ancient Indian queen in ornate royal chamber, sitting at an intricately carved wooden desk, writing on a scroll with a golden quill. Surrounding her are treasure chests overflowing with colorful gemstones (ratnas) - rubies, emeralds, sapphires. Warm candlelight illuminates the scene. The queen wears traditional Manipuri royal attire with gold jewelry. Her expression is wise and mysterious. Art style: Detailed illustration with rich Indian aesthetic, warm color palette dominated by gold, amber, and jewel tones.

Click to zoom

Queen Ratnamanjuri of ancient Manipur had amassed a legendary fortune of precious ratnas. As she wrote her final will, she devised a puzzle that would reveal who truly deserved her treasure.

A grand hall with exactly 100 ornate wooden lockers numbered 1-100 arranged in a 10x10 grid on the wall. Each locker has a brass number plate and an elegant handle. In the foreground, a wise old minister in traditional Indian robes gestures toward the lockers while addressing a crowd of 100 people of various ages (including young prince Khoisnam in the front). The lockers have a vintage, treasure-chest-like appearance. Art style: Detailed illustration with perspective showing depth, warm lighting from torches on the walls.

Click to zoom

"Inside ONE of these lockers lies the entire fortune," announced the minister. "If someone solves this puzzle first, they keep EVERYTHING. Otherwise, it's shared equally among all 100 of you."

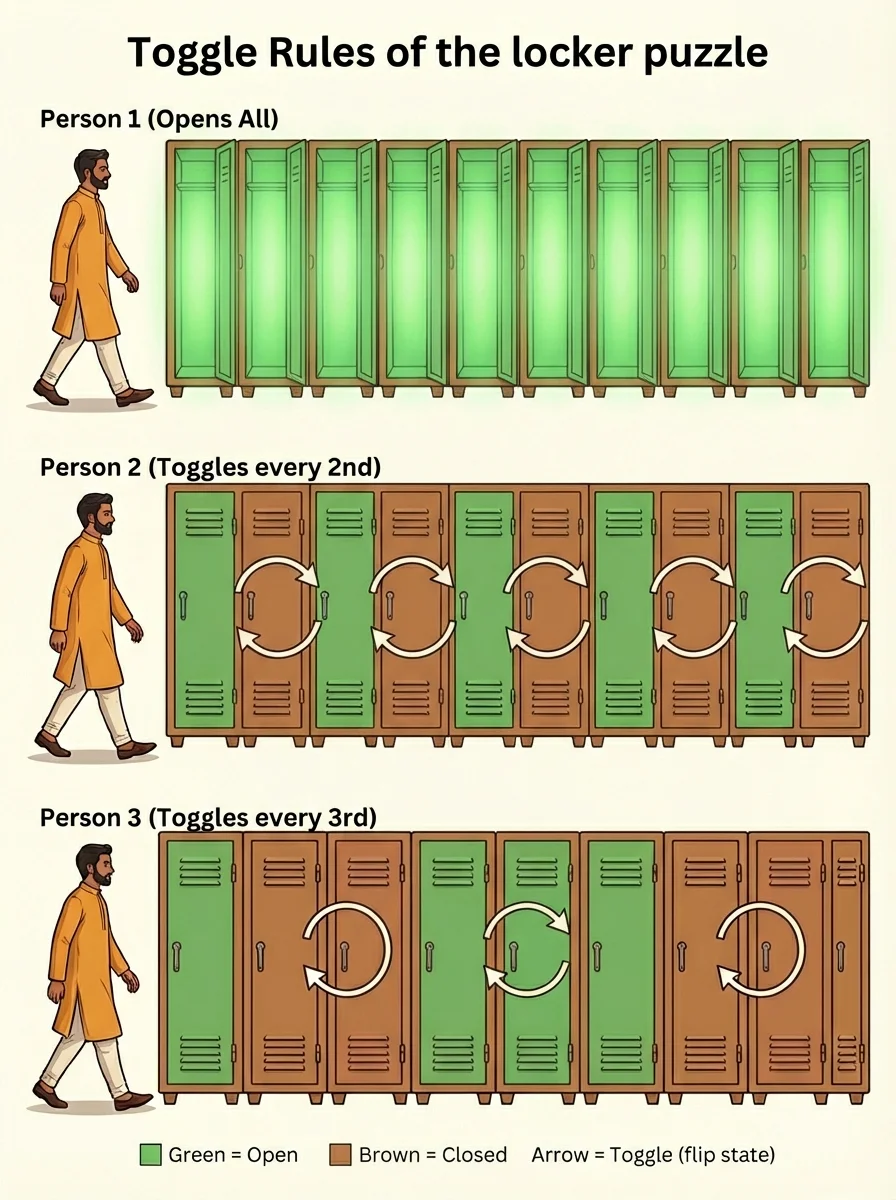
Educational diagram showing the toggle rules with visual examples. Top section: Person 1 walking past lockers 1-10, all shown as OPEN (green). Middle section: Person 2 walking past, with lockers 2,4,6,8,10 being toggled (shown with arrows). Bottom section: Person 3 walking past, with lockers 3,6,9 being toggled. Each section shows a simple figure and the lockers they affect. Include a small legend: Open = green, Closed = red, Toggle = flip the state. Art style: Clean infographic style with clear visual hierarchy, educational look.

Click to zoom

Person 1 OPENS all 100 lockers. Person 2 TOGGLES every 2nd locker (2,4,6...). Person 3 TOGGLES every 3rd (3,6,9...). Toggle means: if open → close it, if closed → open it.

Wide shot showing the 100 people lined up, each with a number badge (1-100). The first few people are actively walking past the lockers doing their toggles. Show motion lines and some lockers in mid-toggle (half-open). The atmosphere is tense and competitive. Some people look confused, some are counting on their fingers. In the corner, young Khoisnam sits calmly with a knowing smile. Art style: Dynamic illustration showing movement, crowd scene with individual expressions visible.

Click to zoom

Each person toggles ONLY the lockers that are multiples of their number. Person 4 toggles 4,8,12... Person 10 toggles 10,20,30... Person 100 only touches locker #100. The tension builds with each turn.

Close-up portrait of young Prince Khoisnam (around 12-14 years old) with a confident, knowing smile. He's sitting cross-legged in a meditative pose while chaos unfolds behind him (blurred figures frantically calculating). Above his head, a thought bubble shows: the numbers 1,4,9,16,25,36,49,64,81,100 glowing with mathematical symbols. His eyes sparkle with intelligence. Traditional Indian prince attire with a small crown. Art style: Character portrait with bokeh background, warm lighting on face, magical/mathematical elements in thought bubble.

Click to zoom

While everyone else scrambled to figure out the answer, young Khoisnam sat peacefully. He had discovered a secret pattern: the answer was hidden in FACTORS and PERFECT SQUARES. What did he see that others missed?

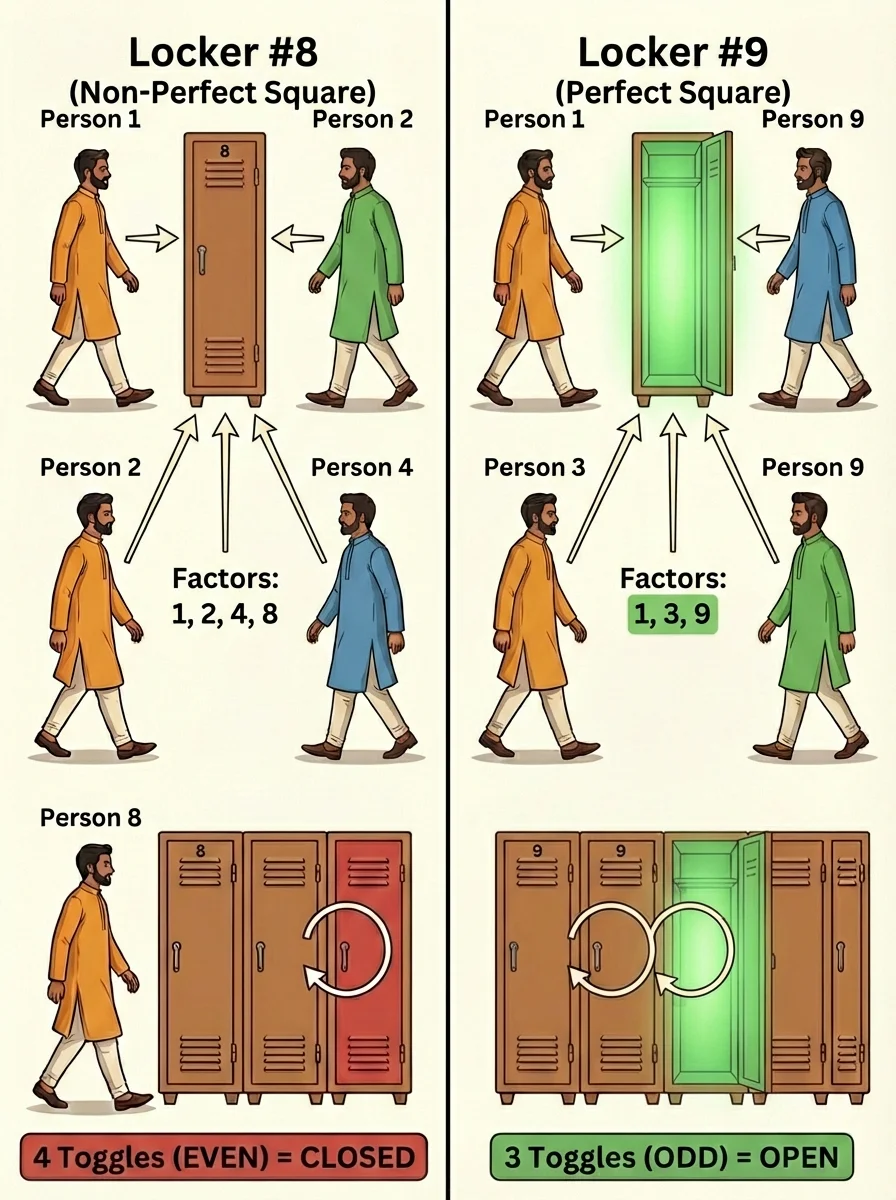
Educational split-screen diagram. LEFT SIDE labeled 'Locker #12': Shows persons 1,2,3,4,6,12 each toggling it (6 arrows pointing at the locker), final state CLOSED. The factors 1,2,3,4,6,12 shown as pairs: (1×12), (2×6), (3×4). RIGHT SIDE labeled 'Locker #9': Shows persons 1,3,9 each toggling it (3 arrows), final state OPEN with golden glow. The factors shown: (1×9), (3×3) with the 3×3 highlighted specially. Text at bottom: 'EVEN toggles = CLOSED, ODD toggles = OPEN'. Art style: Clean educational infographic with clear visual comparison, mathematical notation.

Click to zoom

Locker #12 has factors 1,2,3,4,6,12 — that's 6 toggles (EVEN) → CLOSED. But Locker #9 has factors 1,3,9 — only 3 toggles (ODD) → OPEN! Why does 9 have an odd count? Because 3×3 counts as just ONE factor!

Triumphant finale scene: The 10 winning lockers (numbered 1,4,9,16,25,36,49,64,81,100) are open and glowing with golden light, arranged in a highlighted row. Below each number, show its square root: √1=1, √4=2, √9=3, √16=4, √25=5, √36=6, √49=7, √64=8, √81=9, √100=10. Young Khoisnam stands victoriously in front of the lockers with the treasure. The other relatives look amazed. Text banner: 'PERFECT SQUARES have ODD factors!' Art style: Celebratory illustration with golden lighting effects, mathematical annotations, triumphant mood.

Click to zoom

Only 10 lockers remain open: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 — all PERFECT SQUARES! These are 1², 2², 3², 4², 5², 6², 7², 8², 9², 10². Khoisnam claimed the treasure by understanding the mathematics of factors.

df6842b5...

concept

The Secret: Factors

Understanding why perfect squares have odd number of factors

The Secret: Factors and Toggles

Did you notice the pattern?

Key Insight: Locker #N is toggled by Person K only if K is a factor of N.

Locker #6 toggled by: Person 1, 2, 3, 6 Because 1, 2, 3, 6 are factors of 6!

fe31e466...

quiz

Locker Puzzle Check

Test your understanding of the locker problem

0 / 4

In the 100 lockers problem, how many times is Locker #12 toggled?

Nested pages

1.1 Square Numbers

create

View